Re: ���ԥ�����աʴ����إ����ȡ���Ƽԡ������µ� �������2008ǯ10��14��(��)07��54ʬ28�� |
|
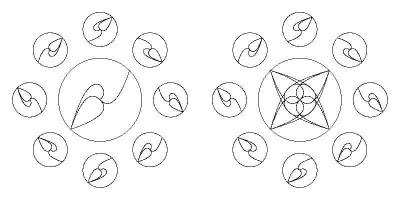
> No.19[��������] �����ͻҤ˥������Ƥߤޤ����� FUNCTION GCD(a,b) !�������� IF b=0 THEN LET GCD=a ELSE LET GCD=GCD(b, MOD(a,b)) END FUNCTION LET r1=8 !����ߤ�Ⱦ�� LET r2=5 !ư���ߤ�Ⱦ�¡���r1*r2>0�ʤ���¦��r1*r2<0�ʤ鳰¦ LET r3=4 !��P�ΰ��֡�ư���ߤ��濴����ˡ���r3=r2�ʤ饵���������ɡ�r3��r2�ʤ�ȥ������� !LET r1=8 !����ߤ�ľ�� r1:r2=2:1 !LET r2=4 !LET r3=r2 !LET r1=12 !�����ƥ����� 4:1 !LET r2=3 !LET r3=r2 !LET r1=5 !������������ 1:1 !LET r2=-5 !LET r3=ABS(r2) !LET r1=4 !�ͥե����� 2:1 !LET r2=-2 !LET r3=ABS(r2) IF r1*r2>0 THEN IF ABS(r1)>ABS(r2) THEN LET sz=MAX(ABS(r1),ABS(r1-r2)+ABS(r3))+1 ELSE LET sz=ABS(r1)+ABS(r3)+1 END IF ELSE LET sz=ABS(r1)+ABS(r2)+ABS(r3)+1 END IF SET WINDOW -sz,sz,-sz,sz !ɽ���ΰ� DRAW grid !��ɸ DRAW circle WITH SCALE(r1) !�礭�ʱ� LET iter=r2/GCD(r1,r2) !����� SET DRAW MODE NOTXOR DIM w(4,4) !���������ɸ����ɺ�ɸ���Ѵ����� MAT w=SHIFT(r1-r2,0) !������ DRAW p(0) WITH w FOR th=0 TO 360*iter !STEP 0.2 !���¤ˤʤ�ʤ�Ĵ�� DRAW p(0) WITH w !��������ä� MAT w=ROTATE(-r1/r2*RAD(th)) * SHIFT(r1-r2,0)*ROTATE(RAD(th)) !�����Ȱ��� DRAW p(1) WITH w !���ɺ�ɸ�ˡ�ư���ߤ���P������ WAIT DELAY 0.02 NEXT th PICTURE p(f) !���������ɸ�θ�������ˡ�ư���ߤ���P������ IF f=1 THEN !�������θ���ơ������P������ SET DRAW MODE OVERWRITE !����disk��NOTXOR��ȿ�Ǥ����ʤ� DRAW disk WITH SCALE(0.2)*SHIFT(r3,0) SET DRAW MODE NOTXOR END IF DRAW circle WITH SCALE(r2) !ư���� PLOT LINES: 0,0; r3,0 END PICTURE END 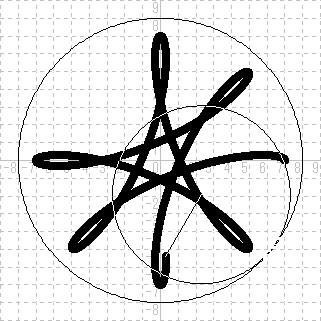
|














���Ǽ��ij���
��Ƽԡ����С����� �������2008ǯ 7��21��(��)09��38ʬ46���ᥤ��ηǼ��Ĥ���Ĵ�ΤȤ�������������Ѥ���������
�ʤ�������500�Ԥޤǽ���뤳�ȤˤʤäƤ��ޤ�����
�¸�Ū�ˤ�251�ԤޤǤ�������ʤ��褦�Ǥ���
Internet Explorer�Ǥ⥤��ǥ�Ȥ��ݻ������ޤ�ɽ������뤳�ȡ�
Ʊ��ͤˤ��Ϣ³���ߤ˵����������뤳�ȡʥ��ѥ��к���
�ʤɡ�������¿���Τǡ�����Ū�ˤ��ܳ�Ū�ʰ�ž�⤢�ꤨ�ޤ���