

相似縮小変換 f1 , f2 に対して,
f 1(D)∪f 2(D) = D
となる図形Dを自己相似図形という。
Dが有界であるものと仮定すれば,Dを描く手続きを次のように作成することで,Dを描くことができる。
Dを描く手続き
f1(D)を描く
f2(D)を描く
手続きの終わり
f1,f2が縮小写像であることから,この再帰手続きを繰り返すと,描くべき図形の直径はディスプレーの解像度に比べて十分に小さくなる。そのとき,問題の図形を1点で代替して描くことができる。
f1が原点を中心とする45°の回転と 1/√2倍の縮小の合成写像, f2が点(1,0)を中心とする45°の回転と1/√2倍の縮小の合成写像である場合, f1 , f2 に対する自己相似図形は, 次のように求められる。
原点を中心とする角αの回転を rotate(α),
原点を中心とする r倍の拡大を scale(r),
x軸方向にa,y軸方向にbの平行移動を shift(a, b)で表し,
変換T1 ,T2の合成をT1*T2で表すと,
f1,f2は,
f1 = rotate(π/4)*scale(1/√2),
f2 = shift(1,0)*rotate(π/4)*scale(1/√2)*shift(1,0)
と表すことができる。
Dを描く手続きのなかでf 1(D)やf 2(D)を描くのに,JIS Full BASICの図形の変換の機能を用いる。
100 PICTURE D(n) 110 IF n=18 THEN 120 PLOT POINTS: 0,0 130 ELSE 140 DRAW D(n+1) WITH ROTATE(PI/4)*SCALE(1/sqr(2)) 150 DRAW D(n+1) WITH SHIFT(-1,0)*ROTATE(PI/4)*SCALE(1/sqr(2))*SHIFT(1,0) 160 END IF 170 END PICTURE 180 SET WINDOW -1/2 , 3/2 , -1 , 1 190 SET POINT STYLE 1 210 DRAW D(0) 220 END
100行から170行までは,図形Dを描くための手続きDを定義する部分である。そして,プログラムの実行は180行から開始される。
180行では,描画領域にx座標の範囲が-1/2から3/2,y座標の範囲が-1から1までとなる座標系を設定している。描画領域の形状は正方形であるので,x座標の幅とy座標の幅とが等しくなるようにしておく。
190行は,120行のplot points文で描かれるマークの形状を・に変更する。
210行は,引数nに0を代入して100行から始まる絵定義(picture)Dを呼び出す文である。100行から始まる絵定義Dで,引数nは再帰の深さを制御するためのものである。140行と150行で再帰的にDを呼び出すときにnを1加算している。nの値が110行のif文で指定している数値18になると再帰呼び出しを終了し,変換された座標系の原点にマークを描く。
140行と150行が,再帰呼び出しを利用してDをf1,f2で変換して描くことによりf1(D)とf 2(D)を描く部分である。
110行で指定する定数は,f1,f2の縮小率sと描画領域の縦横方向のピクセル数pとから決定できる。描くべき図形Dの直径が描画領域の幅より小さいものと仮定すれば,sn<1/pとなるようにnを選ぶことが一応の目安になる。

scale(1,-1)は,x軸に関する対称移動である。
上の例で,f1 を,
f1 =scale(1,-1)*rotate(π/4)*scale(1/√2),
に替えると,次図が得られる。これは,Levy曲線と呼ばれる。
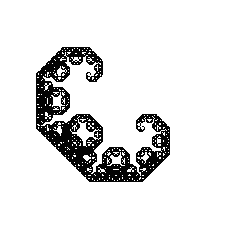
一方,合成する順序を変更して,f1 を,
f1 =rotate(π/4)*scale(1/√2)*scale(1,-1),
に替えると,次図が得られる。
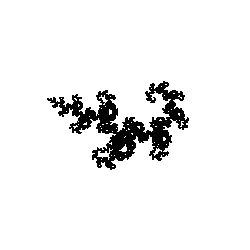
f1 =scale(1,-1)*rotate(π/4)*scale(1/√2),
f2 =shift(-1,0)*rotate(π/4)*scale(1,-1)*scale(1/√2)*shift(1,0)
とすると,次の図が得られる。
一見,何の変哲もない直角2等辺3角形に見えるが,実は,ペアノ曲線である。

ここで,定数を少し変えて,
f1 =scale(1,-1)*rotate(π/6)*scale(1/√3),
f2 =shift(-1,0)*rotate(π/6)*scale(1,-1)*scale(1/√3)*shift(1,0)
とすると,次の図が得られる。
これは,コッホ曲線である。
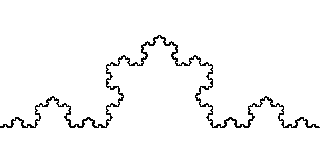
正三角形ABCの各頂点を中心とする1/2倍の縮小写像をそれぞれ,f1,f2,f3とする。
このとき,f1(D)∪f2(D)∪f3(D)=D となる自己相似図形をシルピンスキーのガスケットという。

ここで,3頂点の座標をA(0,0),B(2,0),C(1,√3) とすると,次のプログラムが得られる。
100 PICTURE D(n) 110 IF n=10 THEN 120 PLOT POINTS: 0,0 130 ELSE 140 DRAW D(n+1) WITH SCALE(1/2) 150 DRAW D(n+1) WITH SHIFT(-2,0)*SCALE(1/2)*SHIFT(2,0) 160 DRAW D(n+1) WITH SHIFT(-1,-SQR(3))*SCALE(1/2)*SHIFT(1,SQR(3)) 170 END IF 180 END PICTURE 190 SET WINDOW 0,2,0,2 200 SET POINT STYLE 1 210 DRAW D(0) 220 ENDここで,f1,f2,f3 を各頂点を中心とする1/√3倍の縮小写像と30°の回転の合成に替えると,次の図形が得られる。

この図形も平面を敷き詰めることで有名。
この図形に色を付けてみよう。
BASICでは,
SET COLOR MIX(1) red,green,blue
で,色指標1の実際の色を red,green,blueで指定される色に変えることができる。
ただし,red,green,blueは0以上1以下の数値。
なお,JISは,set color mixを実行したとき,その色指標に対する色が過去にさかのぼって変化するかしないかは処理系定義としている。ここでは,色指標に対する実際の色の割り当てを変更しても,すでに描かれたものには影響しない処理系を用いるものとする。
100 PICTURE tragon(n,red,green,blue) 110 ! print n,red,green,blue 120 IF n=10 THEN 130 SET COLOR MIX (1) red,green,blue 140 set point color 1 150 PLOT POINTS: 0,0 160 ELSE 170 DRAW tragon(n+1,red+2^(-n),green,blue) WITH SCALE(1/SQR(3))*ROTATE(PI/6) 180 DRAW tragon(n+1,red,green+2^(-n),blue) WITH SHIFT(-2,0)*SCALE(1/SQR(3))*ROTATE(PI/6)*SHIFT(2,0) 190 DRAW tragon(n+1,red,green,blue+2^(-n)) WITH SHIFT(-1,-SQR(3))*SCALE(1/SQR(3))*ROTATE(PI/6)*SHIFT(1,SQR(3)) 200 END IF 210 END PICTURE 220 SET WINDOW -2,3,-2,3 230 SET POINT STYLE 1 240 DRAW tragon(1,0,0,0) 250 END
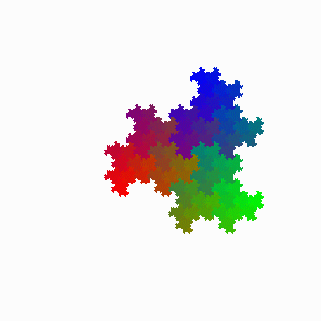
次の図形は,
f1=SCALE(1,-1)*SCALE(1/√3)*ROTATE(π/8)
f2=SHIFT(-1,0)*SCALE(1,-1)*SCALE(2/3)*SHIFT(1,0)
に関する自己相似図形である。

このように,f1,f2の縮小率に差がある場合には,次のプログラムのように,総合の縮小率を表す変数sを用意して,再帰呼び出しを行うごとにそれに縮小率を乗じていくようにするとよい。
100 PICTURE D(s) 110 IF s<0.001 THEN 120 PLOT POINTS: 0,0 130 ELSE 140 DRAW D(s*r) WITH SCALE(1,-1)*SCALE(r)*ROTATE(alfa) 150 DRAW D(s*2/3) WITH SHIFT(-1,0)*SCALE(1,-1)*SCALE(2/3)*SHIFT(1,0) 160 END IF 170 END PICTURE 180 LET alfa=pi/8 190 LET r=1/SQR(3) 200 SET WINDOW -0.5,1.5,-1,1 210 SET POINT STYLE 1 220 DRAW D(1) 230 END
○「フラクタルの数理」,山口昌哉 畑政義 木下淳,岩波講座 応用数学
○「カオスとフラクタル入門」,山口昌哉,放送大学印刷教材
PDF版「(仮称)十進BASICで描く自己相似図形」SelfSim.pdf